LaTeX, a typesetting system celebrated for its capacity to effortlessly blend visual appeal with practicality, remains an essential instrument for both researchers and academics. While its inherent capabilities are impressive, the full potential of LaTeX is revealed through the skillful utilization of its macros. As a researcher in the field of artificial intelligence, I find that I am very often using a set of LaTeX commands, macros and definitions when writing academic papers, and perhaps you will find them useful too.
Introduction
In this blog post, we embark on a journey through the realm of LaTeX macros, unveiling the ten eighteen most essential ones tailored specifically to elevate your computer science paper writing endeavors. From effortlessly formatting algorithms to seamlessly managing references, these macros are poised to revolutionize your writing process, empowering you to focus more on your content and less on formatting intricacies. Whether you’re a seasoned LaTeX user or just beginning to explore its capabilities, this compilation promises to enhance your efficiency, organization, and overall output in the domain of computer science research.
In an earlier post we had a look at ten LaTeX packages, but in this post we will look at commands and macros. So, without further ado, and in no particular order, here are 10 18 useful LaTeX commands, macros and other tips for your writing pleasure.
Commands, macros and other tips
Math modes
When writing math in a paper, you can the LaTeX syntax \( x = 1 \) (or \[ for inline math mode (Wright, 2022). This will sometimes provide better error messages, and having a begin and end point is nice if you ever would like to parse the document with a script. The TeX syntax $ x = 1 $ works as well, and some will say that this is more readable. Read about other subtle differences at Are \ ( and \ ) preferable to dollar signs for math mode?
It is common that LaTeX introduces a line break inside the equation, which might not look great for inline math. You can use curly brackets to avoid the line breaking, for example \({ x = 1 }\).
Dynamic delimiters
Dynamic delimiters in LaTeX are great because they automatically adjust their size to match the content they enclose, ensuring optimal readability and aesthetic presentation of mathematical expressions.
You can manually vary the size of delimiters such as parentheses with \big(, \Big(, \bigg( and \Bigg(.
However, almost always I use dynamically sized delimiters.
1
\left( \sqrt{a}+\sqrt{b}\right )^2
which produces
\[\left( \sqrt{a}+\sqrt{b} \right)^2\]as opposed to
\[( \sqrt{a}+\sqrt{b} )^2\]without using \left( and \right).
I recently learned we can do even better by declaring paired delimiters (Zeng, 2023)! By using the mathtools (Madsen et al., 2022) package we can define a paired braces with
1
\DeclarePairedDelimiter\braces{\lbrace}{\rbrace}
Then we can use the command \braces*{ ...} (note the starred version here) (Zeng, 2023).
Read more about brackets, parantheses and scaling the middle vertical line in Brackets and Parentheses and How to automatically scale \mid within delimiters. Read more about declaring paired delimiters at Automatic left and right commands.
Numbers and units
siunitx (Wright, 2009) is a powerful tool for typesetting and formatting scientific and technical documents. It specializes in handling units, quantities, and numerical values, ensuring proper spacing, alignment, and consistent appearance.
1
2
3
4
5
6
7
8
9
10
11
12
\usepackage{siunitx}
% SI unit setup
\sisetup{
load-configurations = abbreviations,
binary-units = true,
exponent-product=\cdot
}
\DeclareSIUnit{\belmilliwatt}{Bm}
\DeclareSIUnit{\dBm}{\deci\belmilliwatt}
\DeclareSIUnit\px{px}
This allows us to add a number and unit with \SI{52}{\ampere\meter}. A number can be typeset with \num{1e5}. In an earlier post, we looked at using Pandas (pandas development team, 2020; Wes McKinney, 2010 ) to produce nice looking tables with no manual steps, and here we also used the table format S from siunitx.
Spaces and domains
Here are a few definitions of domains that I use.
1
2
3
4
5
\newcommand{\Z}{\mathbb{Z}} % Integer numbers
\newcommand{\R}{\mathbb{R}} % Real numbers
\newcommand{\N}{\mathbb{N}} % Natural numbers or prime numbers
\newcommand{\C}{\mathbb{C}} % Complex numbers
\newcommand{\Np}{\mathbb{N}^+} % Natural numbers including 0
For example \mathbb{N}^+ = \mathbb{N} \setminus \{0\} \(\mathbb{N}^+ = \mathbb{N} \setminus \{0\}\). To denote the empty set, I prefer $\varnothing \(\varnothing\) over \emptyset \(\emptyset\). For this, and many many more notations, see (Siek, n.d.).
Bachmann-Landau notations
Bachmann-Landau notation, a fundamental concept in theoretical computer science and mathematics, offers a concise and standardized way to describe the growth rates of functions and their relationships in mathematical analysis. Named after the mathematicians Paul Bachmann and Edmund Landau (Wikipedia contributors, 2023), this notation employs symbols like \(\mathcal{O}\), \(\Omega\), \(\Theta\), \(o\), \(\omega\) and \(\) to articulate upper, lower, and tight bounds, on the behavior of functions as their inputs become sufficiently large. Bachmann-Landau notation provides a powerful tool for comparing algorithmic efficiencies, predicting performance, and understanding the scalability of mathematical models and algorithms.
Put this in your document preamble.
1
2
\usepackage{amssymb}
\newcommand{\BigO}[1]{\mathcal{O}\!\left(#1\right)}
Then we can you the command ´\BigO{}` like this:
1
\BigO{n\log{}n}
This will produce \(\mathcal{O}\!\left(n \log{n}\right)\). Here is a Complete list of Bachmann-Landau notations. The \! adjusts the spacing to be more pleasing (Thanks u/Tensor_Product_9377!).
Defining new math operators
Operators such as \(\sin\) and \(\cos\) are typeset in a roman font in math mode (Higham, n.d.) . If you need to define a new operator, you can use amsmath to make sure spacing is consistent with the already defined operators.
1
2
3
4
5
6
7
8
9
10
11
\usepackage{amsmath}
\DeclareMathOperator{\tr}{tr}
\DeclareMathOperator*{\Max}{Max}
\DeclareMathOperator{\Prob}{\mathcal{P}}
\DeclareMathOperator{\sgn}{sgn}
\DeclareMathOperator{\DFT}{DFT}
\begin{displaymath}
\Max_{x\in A} f(x) \qquad \End_R V
\end{displaymath}
\def\diag{\mathop{\mathrm{diag}}}
See newcommand vs. DeclareMathOperator and Defining a new log-like function in LaTeX for more information.
Typesetting a definition
Sometimes I see the notation := to denote a definition, and I don’t particularily care for it. I much prefer the overset triangle \triangleq \(\triangleq\) from amssymb.
If you’d rather use an overset text def, here is how to do that.
1
\newcommand\myeq{\mathrel{\overset{\makebox[0pt]{\mbox{\normalfont\tiny\sffamily def}}}{=}}}
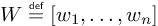
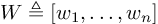
amssymbSee Triangle on top of propto that matches \triangleq, Notation for definition and equivalence, How do I put text over symbols? and Delta-equal to symbol for more information on the topic.
Vectors and matrices
When I studied physics, my preferred way of writing vectors was using \vec{x} \(\vec{x}\). Nowadays, I prefer to use bold symbols for vectors and matrices using the bm package \bm{x} \(\bm{x}\).
See bm package versus \boldsymbol for more information.
Transpose symbol
Here is a controversial topic on which transpose sign to use. I prefer \intercal over T any day of the week, but I agree with the user @Heiko Oberdiek that it is typeset a little too low for capital symbols (such as matrices). For lowercase symbols, just using \intercal looks better to me. See the full discussion on What is the best symbol for vector/matrix transpose?.
1
2
3
4
\makeatletter
\newcommand*{\transpose}}
\newcommand*{\@transpose}[2]{\raisebox{\depth}{$\m@th#1\intercal$}}
\makeatother
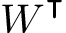
I would like to have one macro for both lowercase and for uppercase symbols alike.
Overbrackets and underbrackets
Brackets, and braces, provide an excellent way of highlighting a part of an equation to be able to explain in better.
1
2
3
\begin{equation}
\min_{\bm{w} \in \mathbb{R}^d} \mathcal{L}(w) \triangleq \min_{\bm{w} \in \mathbb{R}^d} \underbracket[.25pt][12pt]{\sum_{k=1}^K \frac{n_k}{n} \overbracket[.25pt][12pt]{\frac{1}{n_k} \sum_{i \in \mathcal{P}_k} \underbracket[.25pt][10pt]{\ell(\bm{x}_i, y_i, \bm{w})}_{\text{sample}\,i\,\text{loss}}}^{\text{client average loss}}}_{\text{population average loss}}
\end{equation}
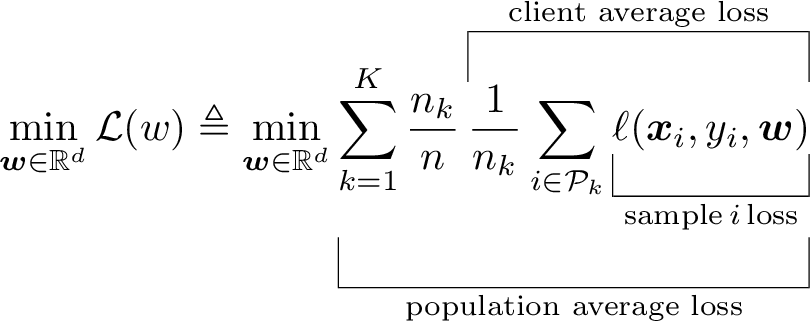
Inline TikZ
Sometimes it is easier to explain something with a small figure instead of creating some notation that is difficult to understand. I like to use this in a figure caption for example. We can use the tikz package (Feuersänger et al., 2014) for this.
1
2
3
4
5
6
7
8
9
10
\documentclass[varwidth=true, border=0pt, convert={outext=.png}]{standalone}
\usepackage{tikz}
\usepackage{xcolor}
\newcommand{\sharedkey}{
\raisebox{-.5 ex}{\tikz{
\draw[fill=blue, draw=white] (0ex,0) arc(90:270:1ex) -- cycle;
\draw[fill=red, draw=white] (0ex,0) arc(90:-90:1ex) -- cycle; }}}
\begin{document}
\(x = \sharedkey\)
\end{document}
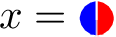
See Tikz picture inline for some other examples.
Figure up top
It is advantageous to put a nice overview figure in the top right corner (Huang, 2018), but it can be a bit fiddly to do so. From StackExchange: Start placing figures on right-hand side column of first page we learn a trick that makes it easier!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
\documentclass{IEEEtran}
\usepackage{lipsum}
\title{My IEEE article}
\author{Author}
\begin{document}
\maketitle
\global\csname @topnum\endcsname 0
\global\csname @botnum\endcsname 0
\begin{abstract} \lipsum[1]\end{abstract}
\section{First Section}
As you can see in Fig~\ref{fig}
\begin{figure}
\centering
\fbox{A nice figure}
\caption{A nice figure}\label{fig}
\end{figure}
\lipsum[1-5]
\end{document}


IEEE references
When writing papers using the IEEE conference template (Shell, 2002) and BibTeX, you can use some interesting trickery to automatically control when et al. will be written out (Shell, 2007) instead of editing the .bib-file. From the IEEE conference template we have that unless there are six authors or more we should print out the names of all the authors.
In the document itself, in the preamble, you need to add
1
\bstctlcite{IEEEexample:BSTcontrol}
At the top of your .bib-file you put this.
1
2
3
4
5
@IEEEtranBSTCTL{IEEEexample:BSTcontrol,
CTLuse_forced_etal = "yes",
CTLmax_names_forced_etal = "6",
CTLnames_show_etal = "1"
}
- Setting
CTLuse_forced_etaltoyestruncates the list of author names and forces the use of “et al.” if the number of authors in an entry exceeds a set limit. CTLmax_names_forced_etalis the value of the maximum number of names that can be present beyond which “et al.” usage is forced. From the IEEE conference template we get that this shall be 6.- When et al. is forced,
CTLnames_show_etalcontrols the number of names that are shown.
See (Shell, 2007) for complete list of parameters and default values.
Citations without line breaks
Citations and references is something that LaTeX and BibTeX do really well. A common way of citing is by writing word~\cite{source} so that there is a non-breaking space between the word and the brackets (assuming IEEE style here). However, when you cite multiple sources, the result is [7]–[9] or [10, 11] which could potetially introduce a line break within the citation itself! To fix this, we need to redefine the \citepunct and \citedash macros that determine what is inserted between the citations. In the first case, we just use a common non-breaking space ~, and in the second the \nolinebreak command prevents line breaking, and \hspace{0pt} allows the following text to start immediately, without inserting any additional space.
1
2
\renewcommand{\citepunct}{,~}
\renewcommand{\citedash}{]--\nolinebreak\hspace{0pt}[}
Typesetting et al.
I like to use a macro to write et al. where we add a penalty to a line break between the two parts.
1
\def\etal.{et\penalty50\ al.} % et al. with correct spacing
See Should “et al.” have a thin or full, non-breaking vs. breaking space?.
Epsilon
In academic writing, particularly in mathematics and related fields, the subtle nuances of notation play a crucial role in conveying precise meanings. This holds true for symbols like “epsilon,” often denoted as either \(\epsilon\) (lunate form) or \(\varepsilon\) (inverted-3 form). While both symbols might appear similar at first glance, they possess distinct roles in communicating mathematical ideas. Epsilon is commonly used as a placeholder for a small positive quantity in calculus and analysis, and is often employed when emphasizing a specific value within a sequence or as an arbitrary small quantity in proofs and formal arguments. The choice between these two symbols illustrates the meticulous attention to detail that characterizes academic writing, where even the slightest distinction can significantly impact the clarity and accuracy of mathematical expressions. Which symbol to use where might be a matter of discussion and source of confusion. See (Wikipedia contributors, 2023) and \varepsilon vs. \epsilon for more information on the two versions.
Imaginary i
The possible ways of typesetting an imaginary \(\mathrm{i}\) are discussed in How should imaginary numbers be typeset?.
I like to use an upright \(\mathrm{i}\), as in (ISO, 2009). Adding a small kern to distance it from an exponent, we can define it as
1
\newcommand{\di}{\mathrm{i}\mkern1mu} % imaginary i in roman and with correct spacing
Bonus tip
Not a LaTeX command, package or macro, but an extremely useful tool - Detexify is a web-based tool designed to help users find the LaTeX command for a specific symbol by drawing it. There is also a Mac OS application!
Related work
There are a few other sites with similar lists, and here are some of my favorites.
- The Art of LaTeX: Common Mistakes, and Advice for Typesetting Beautiful, Delightful Proofs (Zeng, 2023)
- Use Custom LaTeX Macros to Boost Your Writing Productivity (Valero, 2021)
Conclusion
In the world of LaTeX, a vast universe of tools and techniques awaits those who wish to craft elegant mathematical documents. We’ve journeyed together through a mere eighteen tips, each unlocking a new facet of the mathematical prowess of LaTeX. From mastering different math modes to harnessing the power of dynamic limiters, numbers, and units, we’ve delved deep into the intricacies of mathematical typesetting. For anyone wishing to delve deeper into this, I would recommend (Knuth et al., 1989).
As we conclude this exploration, we’re reminded that there’s no shortage of LaTeX packages, macros or syntaxes, nor is there a lack of “top ten” lists showcasing them. However, what truly matters is the journey you embark on with LaTeX — a journey that enables you to bring forth your mathematical visions, share your discoveries, and communicate the wonders of mathematics to the world.
So, whether you’re a seasoned LaTeX user or just beginning your mathematical typesetting adventure, I hope these eighteen tips have been a source of inspiration and knowledge. As you continue your LaTeX endeavors, remember that each equation, each symbol, and each beautifully typeset equation is a testament to the elegance and power of LaTeX. More importantly, the time you spend on typesetting an equation is actually time spent on helping someone else understand it. There’s a universe of mathematical expression waiting to be explored, and LaTeX is your trusty spacecraft to navigate it. Here’s to your mathematical journey, and I hope you’ve enjoyed this ride!
References
- Wright, J. (2022). Some TeX Developments — Math mode. https://www.texdev.net/2022/09/13/math-mode—vs-%5C(-%5C)
- Zeng, F. P. (2023). The Art of LaTeX: Common Mistakes, and Advice for Typesetting Beautiful, Delightful Proofs. https://fanpu.io/blog/2023/latex-tips/
- Madsen, L., Høgholm, M., & The LATEX Project Team. (2022). mathtools – Mathematical tools to use with amsmath. System, 1–38. https://ctan.org/pkg/mathtools
- Wright, J. (2009). siunitx — A comprehensive ( SI ) units package. System, 1–60. https://www.ctan.org/pkg/siunitx
- pandas development team, T. (2020). pandas-dev/pandas: Pandas (latest). Zenodo. https://doi.org/10.5281/zenodo.3509134
- Wes McKinney. ( 2010 ). Data Structures for Statistical Computing in Python . In Stéfan van der Walt & Jarrod Millman (Eds.), Proceedings of the 9th Python in Science Conference (pp. 56–61 ). https://doi.org/ 10.25080/Majora-92bf1922-00a
- Siek, K. LaTeX Formal Methods Reference. Retrieved August 10, 2023, from http://www.cs.put.poznan.pl/ksiek/latexmath.html
- Wikipedia contributors. (2023). Big O notation — Wikipedia, The Free Encyclopedia. https://en.wikipedia.org/w/index.php?title=Big_O_notation&oldid=1168125072
- Higham, N. Top Tips for New LaTeX Users. Retrieved August 11, 2023, from https://nhigham.com/2015/09/29/top-tips-for-new-latex-users/
- Feuersänger, C., Menke, H., & Tantau, T. (2014). TikZ & PGF manual. https://www.ctan.org/pkg/pgf
- Huang, J.-B. (2018). Deep Paper Gestalt. CoRR, abs/1812.0. http://arxiv.org/abs/1812.08775
- Shell, M. (2002). How to use the IEEEtran LATEX class. Journal of LaTeX Class Files, 12.
- Shell, M. (2007). How to Use the IEEEtran BIBTEX Style. Journal of LaTeX Class Files, 12(4), 100–120.
- Wikipedia contributors. (2023). Epsilon — Wikipedia, The Free Encyclopedia. https://en.wikipedia.org/w/index.php?title=Epsilon&oldid=1168559821
- ISO. (2009). ISO 80000-2: Quantities and units — Part 2: Mathematical signs and symbols to be used in the natural sciences and technology (p. 40). pub-iso. https://www.iso.org/standard/31887.html
- Valero, C. S. (2021). Use Custom LaTeX Macros to Boost Your Writing Productivity. https://www.cesarsotovalero.net/blog/use-custom-latex-macros-to-boost-your-writing-productivity.html
- Knuth, D. E., Larrabee, T., & Roberts, P. M. (1989). Mathematical Writing (Vol. 14). Mathematical Association of America. https://jmlr.csail.mit.edu/reviewing-papers/knuth_mathematical_writing.pdf
Suggested citation
If you would like to cite this work, here is a suggested citation in BibTeX format.
@misc{isaksson_2023,
author="Isaksson, Martin",
title={{Martin's blog --- Top LaTeX commands and macros for academic writing (and more)}},
year=2023,
url=https://blog.martisak.se/2023/08/11/top-latex-commands/,
note = "[Online; accessed 2024-10-03]"
}
